mojavy.com

ベイズの定理から見るガン検査

November 12, 2013 at 03:01 AM | categories: statistics |

http://www.huffingtonpost.jp/2013/11/10/cancer-test_n_4252707.html

高校生がすい臓がん発見の画期的方法を開発したという記事が話題になってます。

この検査法の改善が統計的にどういう意味をもつのか実際にベイズの定理をつかって計算してみます。

ここでは以下のような問題を考えることとします。

あるガン検査法は、被験者ががんの場合はp1の確率で陽性になり、被験者ががんでなければp2の確率で陰性になります。被験者ががん患者である確率がp3のとき、がん患者が検査の結果実際に陽性だと判定される確率を求めなさい。

Xを被検査者はガンであるという事象、Yを検査の結果が被検査者はガンであると示す事象として、それぞれ以下のように置き換えることができます。

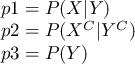
ただし、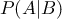はBが起こったときにAが起こる確率(条件付き確率)、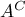はAが起こらないという事象(補事象)を表します。

求めたい確率は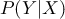なので、ベイズの定理より

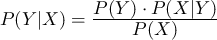
ここで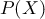は検査結果が真陽性となる確率と偽陰性となる確率を足したものなので、

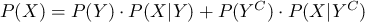
また、

なので、

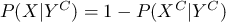
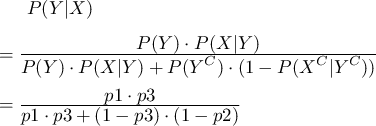
となります。

以上の結果に実際に値をあてはめてみます。

2008年のすい臓がん推定患者数は29584 ¹、同年の人口は127692000 ²なので、p3=0.23168 * 10^-3。また、簡単のためにp1, p2をひとまとめに誤検出の確率と仮定してp1=p2=qおくと、P(Y|X)が70%となるようなqは、q=0.99990となります。

このことから、99.99%の精度をもつ検出方法でも実際には30%も見逃してしまうということがわかります。

さらに、「400倍の精度で検査できる」という部分を誤検出の確率が400分の1になったという意味だと解釈して、 q'=1-(1-q)/400とおいてがん患者が検査の結果実際に陽性だと判定される確率を再度計算するとP(Y|X)=0.99892となります。

つまり30%見逃していたのが1%程度まで減ったということです。これはすばらしい成果といえるのではないでしょうか。

最初は30%も見逃すとかどんなひどい検査だったんだ、などと思ってしまうかもしれませんが、上記の計算で実際はそれほど単純な話ではないことがわかると思います。